“Differentiation” is used to mean so many different things the term is effectively meaningless. Most are hard to do, take a lot more teacher time/effort and are unlikely to benefit students.
There is my opening statement and I’d be interested in your thoughts. It is not actually mine, borrowed for the purpose of this enquiry.
Let’s set aside the inherent, prescriptive and structural forms of differentiation already imposed on our teaching: the curriculum, year groups, group sizes, two, three, even five year curriculum designs, (Amanda Spielman), separating academic and vocational paths and let’s agree to set aside genuine exceptions where differentiation may be required, like when a teaching a visually impaired student who might use a text reader or laptop… let’s narrow the focus towards instructional differentiation. Even then, it remains a slippery customer; groups, outcome, task, pace, level of support. So we refine our focus again, to the much expected differentiation focus of – by task.
Within this frame, the OECD sends out a questionnaire to teachers in member countries and one of the questions they ask teachers is how often do they give “different work to the pupils, who have difficulty learning and/or to those who can advance faster.” I have noted previously that high-performing PISA countries tend to do less of this than lower performing ones.
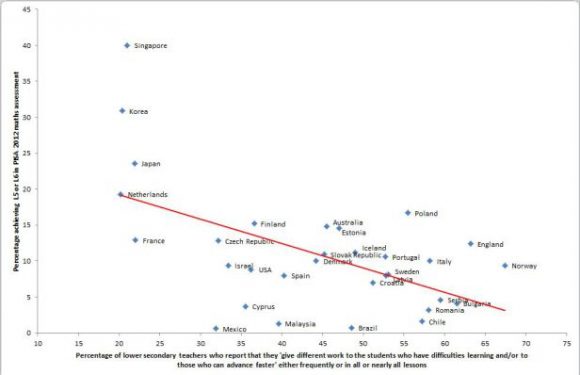
Alternatively, differentiation of work within classes is much less prevalent in top-performing countries than it is in England. See Report on research into maths and science teaching in the Shanghai region). If only differentiation were that simple to define.
Now let’s zoom in on a class. Respectfully, this is just a snapshot to help me illustrate my thinking, though it was a real lesson.
A Year 4 class. The pupils are already seated by the previous teacher? Is that a lack of differentiation for what is to follow – a maths lesson? It is a small, mixed attainment group. Does that mean there needs to be less or more differentiation? Do we concern ourselves with the summer born?
The lesson: an interview lesson with a wonderfully vibrant and enthusiastic teacher. The lesson starts with a recap for all pupils on shapes and an opening question that prompts every pupil to think about shapes. A maths thunk kind of question. It is a relatively low bar, no differentiation – safe. Or is that differentiation, setting a easy question to get the pupils to trust you? Connections made with the pupils, we are off to a good start.
There is some critical input and demonstration – “how to find the area of a shape.” Expectation for attention are non-negotiable, a lack of empathy for the learning needs of pupil X? Questions are directed, clearly according to the class profile. That is, differentiation by question. Conversation is encouraged for this new topic – is that differentiation? “321 – talking done.” Allowing pupils to learn from one another? To check their understanding? Is that differentiation?
Now – new tier three vocabulary. “What about these shapes?” Rectilinear (it is new to me too). Verbal repetition of the term aids it’s adoption by the pupils. A consolidation activity with post notes (squares) confirms that pupils can make their own rectilinear shapes and confirm their common understanding of “right-angles.” Some pupils get support? Some ask questions? Differentiation?
The teacher zooms the room… some pupils get a pointer? Some get a thumbs up? Some get – “There’s a party over here,” and jazz hands meets bunny game – identification. Some pupils join the party? Differentiation?
Back to the board. An exposition on how to find the area of a rectilinear shapes. Here is the clever link, the area of these rectilinear shapes is measured in “cm squares”[d]. The demonstration on the board uses squares (just like the post-it-notes) that are moved together, to fit, to replicate a shape created by one of the pupils. This is purposeful and the connection is made public. The young girl, lacking in confidence, noticeable sits up straight. She physically grows two inches. Is that differentiation?
Now for the hard-at-work, deliberate practice… working out the area of rectilinear shapes worksheet, “differentiated by entry.” Pupils self select their level of challenge.
Another check-in from the teacher and room-zoom.
Now for the big reveal. Out come the zoo animals, with labels showing the area value of the enclosure that they require. Now we are introduced to metres squared. Pupils have to design and calculate the rectilinear enclosures. This is very exciting and there are challenge animals too! Definitely differentiation.
Some pupils select animals that have simple areas to design and calculate (eg 24m2), others have more challenging solutions to find (87m2). Which animal pupils selected was completely at random. Here, the teacher set an irregular bar, though remember a high bar is available via the challenge animals.
As an observer I have absolutely no clue if this was purposeful or not? I will have to ask. If it was, is it differentiation?
The lesson is humming with activity and pupils are talking about their animals and design of the enclosure. They are exploring different rectilinear designs and undertaking many calculation, (multiplication and addition). “321 talking is done.” The keep terms are repeated, the process is affirmed and quickly they are back to work.
The pupils describe the lesson as one of their “best maths lesson ever.”
I would dare anyone, other than the teacher who prepared that lesson, to be able to assign a quantitative value to differentiation in that lessons. Even to accurately answer the degree to which “different work” was given to the pupils”who have difficulty learning and/or to those who can advance faster.”
I am neither an advocate nor a detractor for differentiation; I am puzzled by our determined insistence on differentiation in England, given differentiation’s unquestionable and ever-fluid morphology within most lessons. Given that we know that the most important difference between pupils, is what they already know.
“If I had to reduce all of educational psychology to just one principle, I would say this: The most important single factor influencing learning is what the learner already knows. Ascertain this and teach him accordingly” (Ausubel, 1968 p. vi).
I am particularly concerned with our insistence on differentiation by task. I am, differentiating my levels of concern – for differentiation. How ironic.
As not to sit on the fence, to nail my colours to the mast. In most settings I would advocate teaching to a ‘rising tide’ principle – that a rising tide lifts all ships.
- Teach with high expectation for all pupils. Expect and secure the pupils full attention.
- All pupils complete the same work. Invest in planning and thinking through the learning you anticipate will result.
- Support where needed. Targeted, accelerated intervention if support is insufficient.
- Make the connections explicit for learners. Interrogative their understanding. The craft of teaching.
- Expect pupils to be able to retrieve knowledge.
- Evaluate one’s own learning.
The expectation and belief that every student is capable of learning and that there are no intellectual boundaries to knowledge; an almost Confucian work ethic. What I have previously and lazily referred to, as teaching to the top.
Find out what they know. Ask or quiz the pupils. Pre-test, probe their understanding. Use formative assessment often. Both strategies were event in the Year 4 case study shared. Decide what to do with this information and how you will use it to leverage their motivation and attention.
To be concise: I reject categorising learning – that is a no to “all, most, some.” Differentiation by target grade (these are far to broad for a single lesson topic).
I would therefore reflect and suggest that there really is only two practical approaches to dealing with the range of attainment found in every class – that is, a) to use inclusive differentiation, with formative and responsive teaching.
b), to differentiate through ‘targeted intervention or catch-up provision.’ That is for pupils who maybe be excelling well beyond their peers, or pupils who have not grasped an essential component that proves to inhibit onward learning.
Note, that in the later case, these pupils need to be learning at a faster or accelerated pace than that of the class,for the intervention to be considered successful and for the pupil to be in a strong position to return.
As with all aspects of instructional practice, I remind myself on the inter-connectedness and complexity of our profession. Any decision you make, to differentiate or not, will have consequences.
I certainly thanked and recognised the teachers sincere efforts in the Year 4 lesson I outlined, however, we can not reasonable expect our teachers to plan, prepare and deliver six of the “best maths lesson ever,” every day.
Differentiation is discrimination. Discuss?
More food for thought here, in the article that Prof Rob Coe references form the image.



